[用JS來寫演算法和了解資料結構] Day1 演算法的好壞評量標準 Big O

前言

這個系列主要是想自我挑戰30天用學資料結構和演算法。因為不是資訊本科生，對資料結構的理論一知半解，藉由筆記更加深印象。會搭配一個我很喜歡的前端工程師Hannah分享的鐵人賽文章，來做練習。這邊因為是我個人練習學習，順序或時間可能會跟Hannah的文章不一樣。

• 前端工程師用 javaScript 學演算法
• Data Structures and Algorithms (DSA)

會使用或參考到的資源：

• Big-O Cheat Sheet
• LeetCode
• Codility
• CSPIRATION
• leetcode 解題之路
• 程式麻瓜的程式知識課

演算法的好壞評量標準

兩個評量演算法好壞的指標：

1. 時間複雜度 (Time complexity)
2. 空間複雜度 佔用記憶體空間 (Space complexity)
3. 易讀性 (Readable)

時間複雜度 Time complexity

用來評斷演算法執行的快慢，一般用大 O 符號(Big O notation、BigO)來表示，用來描述一個演算法在輸入 n 個東西時，總執行時間與 n 的關係。

舉個例子，來到書店想買一本書XXX，但架子上有大概100本書，兩種找法：

1. 一本一本找，若1本花費1分鐘，10本花費10分鐘，100本花費100分鐘，n本花費n分鐘，時間複雜度是Big O(n)
2. 直接用電腦根據索引找到書的位置，不管幾本都只花費了1分鐘，時間複雜度是Big O(1)

Big O

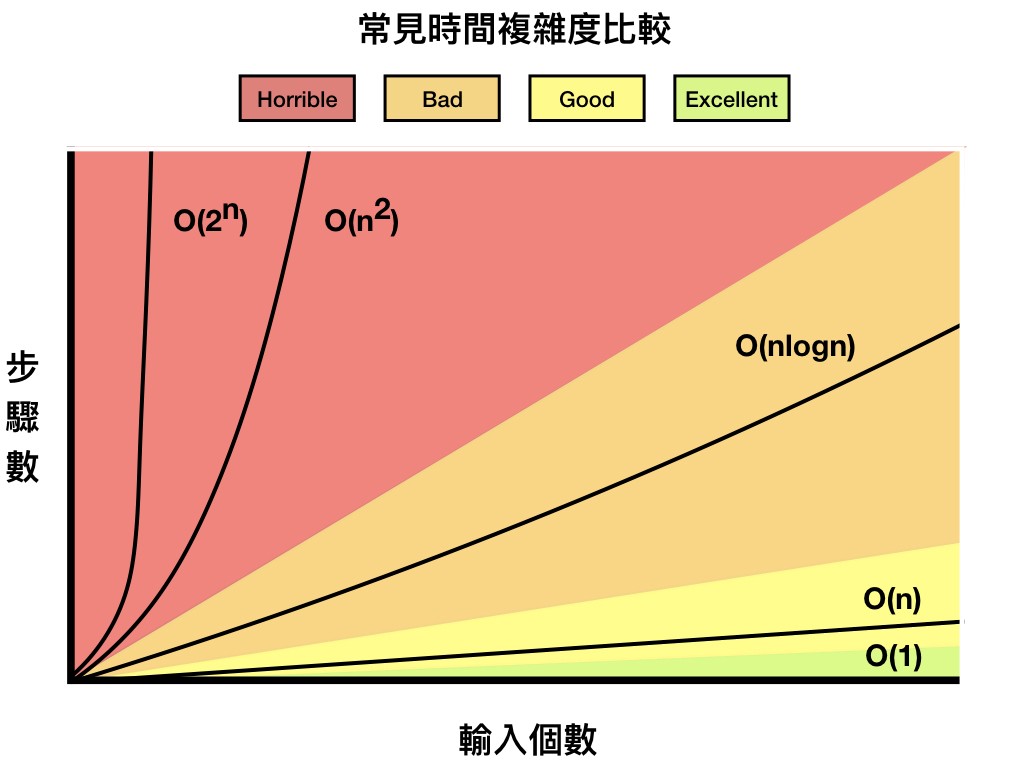
圖片來源

• 程式麻瓜的程式知識課

時間複雜度 從好到不好

1. Constant Time — O(1) - 陣列讀取 (no loops)
2. Logarithmic Time — O(log n) - Binary Search 二分搜索
3. Linear Time — O(n) - 簡易搜索 (for loops, while loops through n items)
4. Linearithmic Time — O(n log n) - 合併排序、快速排序 (usually sorting operations)
5. Quadratic Time — O(n^2) (O n squared / power of 2) - 選擇排序、氣泡排序 (every element in a collection needs to be compared to ever other element. Two
   nested loops)
6. Exponential Time — O(2^n) - 費波那契數列 (recursive algorithms that solves a problem of size N)
7. Factorial - O(n!) - (you are adding a loop for every element)

Iterating through half a collection is still O(n)
Two separate collections: O(a * b)

• 時間複雜度 wiki

• Big-O Cheat Sheet

• 越不好代表程式的步驟次數越高，而非執行時間

1個步驟 Big O(1)

x = 10

11個步驟(宣吿1次+回圈10次) Big O(n)

x = 10
for i from 1 to x:
    print("你好！")

21個步驟(宣吿1次+回圈10次*2次) Big O(n^2)

x = 10
for i from 1 to x:
    print("你好！")

for i from 1 to x:
    print("Hi")

Big O(log n)
假設 n 為 81 個，那麼只要 9 個步驟完成，則是Big O(log n)，例子是二分搜索binary search。

時間限制 Time limit

• n <= 1 000 000, the expected time complexity is O(n) or O(n log n)
• n <= 10 000, the expected time complexity is O(n^2)
• n <= 500, the expected time complexity is O(n^3)

重點

• 大 O 符號：用來描述演算法在輸入 n 個東西時，所需時間與 n 的關係
• 演算法的速度不是以時間計算，而是以步驟次數

What Can Cause Time in a Function?

• Operations (+, -, *, /)
• Comparisons (<, >, ==)
• Looping (for, while)
• Outside Function call (function())

Rule Book

Rule 1: Always Worst Case

Rule 2: Remove Constants

Rule 3:

• Different inputs should have different variables: O(a + b)
• A and B arrays nested would be: O(a * b)

• + for steps in order
• * for nested steps

Rule 4: Drop Non-dominant terms

function printAllNumbersThenAllPairSums(numbers) {
    console.log("these are the numbers:");
    numbers.forEach(function(number) {
      console.log(number);
    });
  
    console.log("and these are their sums:");
    numbers.forEach(function(firstNumber) {
      numbers.forEach(function(secondNumber) {
        console.log(firstNumber + secondNumber);
      });
    });
  }
  
  printAllNumbersThenAllPairSums([1, 2, 3, 4, 5]); // O(n^2)

空間複雜度 Space complexity

What Causes Space Complexity?

• Variables
• Data Structures
• Function Call
• Allocations

學習與參考資料

• 前端工程師用 javaScript 學演算法
• Data Structures and Algorithms (DSA)
• Master the Coding Interview: Data Structures + Algorithms